Birkhoff's axioms
In 1932, G. D. Birkhoff created a set of four postulates of Euclidean geometry sometimes referred to as Birkhoff's axioms. These postulates are all based on basic geometry that can be confirmed experimentally with a scale and protractor. Since the postulates build upon the real numbers, the approach is similar to a model-based introduction to Euclidean geometry. Other often-used axiomizations of plane geometry are Hilbert's axioms and Tarski's axioms.
Birkhoff's axiom system was utilized in the secondary-school text Basic Geometry (first edition, 1940; see References).
Postulates
Postulate I: Postulate of Line Measure. A set of points {A, B, ...} on any line can be put into a 1:1 correspondence with the real numbers {a, b, ...} so that |b − a| = d(A, B) for all points A and B.
Postulate II: Point-Line Postulate. There is one and only one line, ℓ, that contains any two given distinct points P and Q.
Postulate III: Postulate of Angle Measure. A set of rays {ℓ, m, n, ...} through any point O can be put into 1:1 correspondence with the real numbers a (mod 2π) so that if A and B are points (not equal to O) of ℓ and m, respectively, the difference am − aℓ (mod 2π) of the numbers associated with the lines ℓ and m is 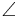 AOB. Furthermore, if the point B on m varies continuously in a line r not containing the vertex O, the number am varies continuously also.
AOB. Furthermore, if the point B on m varies continuously in a line r not containing the vertex O, the number am varies continuously also.
Postulate IV: Postulate of Similarity. Given two triangles ABC and A'B'C' and some constant k > 0, d(A', B' ) = kd(A, B), d(A', C' ) = kd(A, C) and 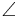 B'A'C' = ±
B'A'C' = ±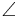 BAC, then d(B', C' ) = kd(B, C),
BAC, then d(B', C' ) = kd(B, C), 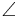 C'B'A' = ±
C'B'A' = ±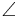 CBA, and
CBA, and 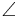 A'C'B' = ±
A'C'B' = ±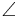 ACB.
ACB.
References
- Birkhoff, George David. 1932. "A Set of Postulates for Plane Geometry (Based on Scale and Protractors)," Annals of Mathematics 33.
- Birkhoff, George David and Ralph Beatley. 1959. Basic Geometry 3rd ed. Chelsea Publishing Co. [Reprint: American Mathematical Society, 2000. ISBN 9780821821015]